作者:桂。
时间:2017-04-04 08:13:14
链接:
声明:欢迎被转载,不过记得注明出处哦~

【读书笔记11】
前言
西蒙.赫金的《自适应滤波器原理》第四版第八章:最小二乘法。全文主要包括:
1)矩阵方程问题描述;
2)最小二乘法;
3)最小二乘与最大似然的关系;
4)最小二乘与梯度下降的关系;
内容为自己的学习记录,其中有借鉴他人的地方,最后一并给出链接。
一、矩阵方程问题描述
A-基本问题描述
许多问题都可以建模成矩阵方程:
${\bf{Ax}} = {\bf{b}}$
其中根据向量![]() 和矩阵
和矩阵![]() 的不同,矩阵方程的求解主要分为以下三类问题:
的不同,矩阵方程的求解主要分为以下三类问题:
1)超定矩阵方程;m>n,$\bf{b}$和$\bf{A}$均已知,其中之一或二者可能存在观测误差、干扰;
2)盲矩阵方程:仅向量$\bf{b}$已知,矩阵$\bf{A}$未知;
3)欠定稀疏矩阵方程:m<n,$\bf{b}$和$\bf{A}$均已知.
每一类问题,都有对应的方法:如对于超定矩阵方程,观测结果足够多,方程个数大于未知数个数,对应矩阵通常列满秩(不绝对),可以利用最小二乘得到唯一确定解;对于欠定矩阵方程,方程个数小于未知数个数,得出的解有多种可能,所以通常需要添加约束——例如稀疏性,虽然解有多种,最稀疏的可能只用一种,这要就得到了唯一确定解。给出问题与对应求解的示意图:
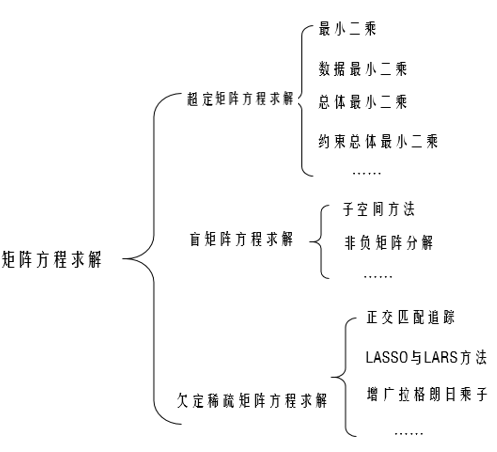
多说一句,例如对于欠定系数矩阵求解,核心问题为:
![]()
这也是稀疏表示和压缩感知的核心问题,由于不免带有噪声,问题通常松弛为:
![]()
B-最小二乘问题
最小二乘根据噪声类型的不同,可以分为:普通最小二乘、数据最小二乘、总体最小二乘。
- 普通最小二乘(Ordinary least squares, OLS)
此时,向量$\bf{b}$(观测向量)带有误差,对应的问题是:
- 数据最小二乘(Data least squares,DLS)
此时,数据矩阵$\bf{A}$带有误差,对应的问题是:
- 总体最小二乘(Total least squares, TLS)
此时,数据矩阵$\bf{A}$和数据矩阵$\bf{A}$都带有误差,对应的问题是:
本文仅分析超定方程情况,且只讨论普通最小二乘(OLS)问题。
二、普通最小二乘求解
普通最小二乘也常被简称为:最小二乘法,但细化问题后其实有些乱,这里仍打算采用普通最小二乘这一说法。
问题描述:
![]()
求偏导:
![]()
这下就熟悉啦,直接走你,就得到常见的表达式:
![]()
怎么错了?这里只是超定方程(m>n),并没有说列一定满秩,所以分两种情况讨论:
情况1:列满秩,rank($\bf(A) $) = n
此时 $\left( {
{ {\bf{A}}^T}{\bf{A}}} \right)$可逆,对应的解唯一,从而有:![]()
情况2:秩亏缺,rank($\bf(A) $) < n
这种情况下,需要借助Moore-Penrose进行广义逆求解,在前文已有介绍,从而有:
![]()
秩亏缺情况下,得到的解不再是唯一的,但基于Moore-Penrose的解是唯一的,这就不免有一个问题——它是增加了何种约束?这里直接给出结论:此时的解为最小范数最小二乘解(minimum norm least squares solution),或者说此时向量对应欧式距离最短.证明可参考:张贤达《矩阵分析与应用第2版》p67.
三、普通最小二乘与最大似然
给出数学模型(以多项式拟合为例,N次拟合,共M组样本点):
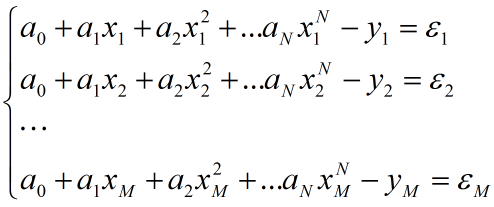
普通最小二乘准则函数:
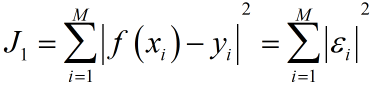
最大似然准则:
假设误差均服从(0,$\delta^2$)的正态分布,则有似然函数:
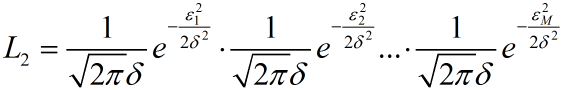
求对数之后,最大似然准则函数等价于:

二者等价。
四、最小二乘与梯度下降
上文一个大前提就是方程可以转化为线性变换:
${\bf{Ax}} = {\bf{b}}$
但很多时候不能实现问题的转化,非线性没有闭式解,这个时候仍然可以借助梯度下降求解,。梯度下降是迭代的方式去逼近最优解,虽然可能是局部最优;而最小二乘是利用矩阵的形式直接得出结果。
参考:
- 张贤达《矩阵分析与应用》.